What Happens to an Electromagnetic Wave When the Frequency Is Doubled?

April 02, 2022 Post a Comment

Electromagnetic Waves

109 Energy Carried by Electromagnetic Waves

Learning Objectives

By the terminate of this section, you will be able to:

Express the time-averaged free energy density of electromagnetic waves in terms of their electric and magnetic field amplitudes
Calculate the Poynting vector and the energy intensity of electromagnetic waves
Explicate how the energy of an electromagnetic wave depends on its aamplitude, whereas the free energy of a photon is proportional to its frequency

Anyone who has used a microwave oven knows at that place is energy in electromagnetic waves. Sometimes this energy is obvious, such as in the warmth of the summertime Sun. Other times, it is subtle, such as the unfelt free energy of gamma rays, which tin destroy living cells.

Electromagnetic waves bring energy into a organization by virtue of their electrical and magnetic fields. These fields can exert forces and move charges in the organisation and, thus, practice piece of work on them. Still, in that location is energy in an electromagnetic moving ridge itself, whether it is absorbed or not. In one case created, the fields carry free energy abroad from a source. If some energy is later absorbed, the field strengths are diminished and anything left travels on.

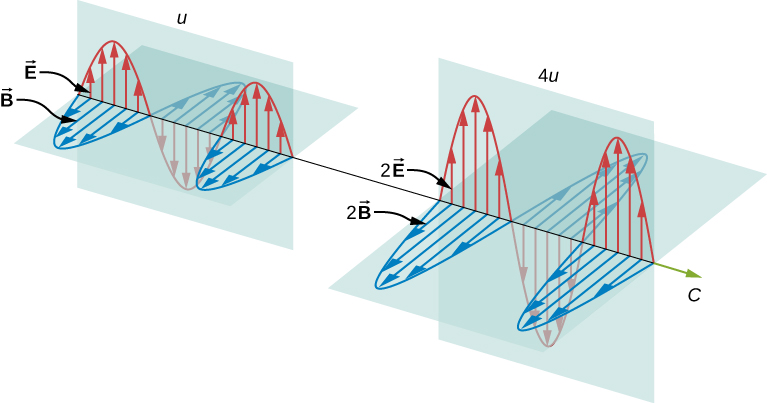
Clearly, the larger the force of the electric and magnetic fields, the more work they can practice and the greater the energy the electromagnetic wave carries. In electromagnetic waves, the amplitude is the maximum field strength of the electrical and magnetic fields ((Figure)). The wave energy is determined by the moving ridge amplitude.

Energy carried by a wave depends on its amplitude. With electromagnetic waves, doubling the E fields and B fields quadruples the free energy density u and the energy flux uc.

Figure on the left shows an electromagnetic wave with electric field E and magnetic field B. It is labeled u. Figure on the right shows an electromagnetic wave with electric field 2E and magnetic field 2B. Here, the amplitudes of the sine waves are doubled. The wave is labeled 4u.

For a plane wave traveling in the direction of the positive x-axis with the phase of the wave chosen so that the wave maximum is at the origin at $t=0$ , the electric and magnetic fields obey the equations

$\begin{array}{c}{E}_{y}\left(x,t\right)={E}_{0}\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}\left(kx-\omega t\right)\hfill \\ {B}_{z}\left(x,t\right)={B}_{0}\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}\left(kx-\omega t\right).\hfill \end{array}$

The energy in whatever part of the electromagnetic wave is the sum of the energies of the electrical and magnetic fields. This free energy per unit book, or free energy density u, is the sum of the free energy density from the electric field and the free energy density from the magnetic field. Expressions for both field energy densities were discussed earlier ( ${u}_{E}$ in Capacitance and ${u}_{B}$ in Inductance). Combining these the contributions, we obtain

$u\left(x,t\right)={u}_{E}+{u}_{B}=\frac{1}{2}{\epsilon }_{0}{E}^{2}+\frac{1}{2{\mu }_{0}}{B}^{2}.$

The expression $E=cB=\frac{1}{\sqrt{{\epsilon }_{0}{\mu }_{0}}}B$ then shows that the magnetic energy density ${u}_{B}$ and electrical energy density ${u}_{E}$ are equal, despite the fact that changing electric fields mostly produce only small magnetic fields. The equality of the electrical and magnetic free energy densities leads to

$u\left(x,t\right)={\epsilon }_{0}{E}^{2}=\frac{{B}^{2}}{{\mu }_{0}}.$

The energy density moves with the electric and magnetic fields in a similar style to the waves themselves.

Nosotros can detect the rate of ship of energy by considering a small fourth dimension interval $\text{Δ}t$ . Equally shown in (Figure), the energy contained in a cylinder of length $c\text{Δ}t$ and cross-sectional area A passes through the cross-sectional aeroplane in the interval $\text{Δ}t.$

The free energy $uAc\text{Δ}t$ contained in the electric and magnetic fields of the electromagnetic moving ridge in the volume $Ac\text{Δ}t$ passes through the area A in time $\text{Δ}t$ .

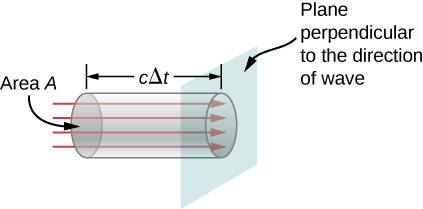
Figure shows a cylinder of length c delta t and cross sectional area A. Arrows indicate the direction of a wave to be along the length of the cylinder. A plane is shown perpendicular to the direction of wave.

The energy passing through area A in time $\text{Δ}t$ is

$u\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\text{volume}=uAc\text{Δ}t.$

The energy per unit surface area per unit fourth dimension passing through a plane perpendicular to the wave, called the energy flux and denoted past Due south, can exist calculated by dividing the free energy by the surface area A and the fourth dimension interval $\text{Δ}t$ .

$S=\frac{\text{Energy passing area}\phantom{\rule{0.2em}{0ex}}A\phantom{\rule{0.2em}{0ex}}\text{in time}\phantom{\rule{0.2em}{0ex}}\text{Δ}t}{A\text{Δ}t}=uc={\epsilon }_{0}c{E}^{2}=\frac{1}{{\mu }_{0}}EB.$

More generally, the flux of energy through any surface also depends on the orientation of the surface. To have the management into business relationship, nosotros introduce a vector $\stackrel{\to }{S}$ , called the Poynting vector, with the post-obit definition:

$\stackrel{\to }{S}=\frac{1}{{\mu }_{0}}\stackrel{\to }{E}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\stackrel{\to }{B}.$

The cross-product of $\stackrel{\to }{E}$ and $\stackrel{\to }{B}$ points in the direction perpendicular to both vectors. To confirm that the direction of $\stackrel{\to }{S}$ is that of wave propagation, and not its negative, render to (Figure). Notation that Lenz's and Faraday'due south laws imply that when the magnetic field shown is increasing in fourth dimension, the electric field is greater at x than at $x+\text{Δ}x$ . The electric field is decreasing with increasing 10 at the given time and location. The proportionality between electric and magnetic fields requires the electric field to increment in time forth with the magnetic field. This is possible only if the moving ridge is propagating to the right in the diagram, in which case, the relative orientations bear witness that $\stackrel{\to }{S}=\frac{1}{{\mu }_{0}}\stackrel{\to }{E}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\stackrel{\to }{B}$ is specifically in the direction of propagation of the electromagnetic wave.

The energy flux at any place besides varies in time, as can be seen by substituting u from (Figure) into (Figure).

$S\left(x,t\right)=c{\epsilon }_{0}{E}_{0}^{2}{\text{cos}}^{2}\left(kx-\omega t\right)$

Because the frequency of visible light is very high, of the order of ${10}^{14}\phantom{\rule{0.2em}{0ex}}\text{Hz,}$ the free energy flux for visible lite through whatever area is an extremely speedily varying quantity. Most measuring devices, including our eyes, detect merely an average over many cycles. The time average of the energy flux is the intensity I of the electromagnetic moving ridge and is the ability per unit of measurement expanse. It tin exist expressed by averaging the cosine office in (Figure) over i complete bike, which is the same as time-averaging over many cycles (here, T is ane period):

$I={S}_{\text{avg}}=c{\epsilon }_{0}{E}_{0}^{2}\frac{1}{T}\underset{0}{\overset{T}{\int }}{\text{cos}}^{2}\left(2\pi \frac{t}{T}\right)dt.$

Nosotros tin can either evaluate the integral, or else annotation that because the sine and cosine differ merely in phase, the average over a complete cycle for ${\text{cos}}^{2}\left(\xi \right)$ is the same as for ${\text{sin}}^{2}\left(\xi \right)$ , to obtain

$〈{\text{cos}}^{2}\xi 〉=\frac{1}{2}\phantom{\rule{0.2em}{0ex}}\left[〈{\text{cos}}^{2}\xi 〉+〈{\text{sin}}^{2}\xi 〉\right]=\frac{1}{2}〈1〉=\frac{1}{2}.$

where the angle brackets $〈\text{⋯}〉$ stand for the time-averaging operation. The intensity of calorie-free moving at speed c in vacuum is then constitute to exist

$I={S}_{\text{avg}}=\frac{1}{2}c{\epsilon }_{0}{E}_{0}^{2}$

in terms of the maximum electric field strength ${E}_{0},$ which is as well the electric field aamplitude. Algebraic manipulation produces the relationship

$I=\frac{c{B}_{0}^{2}}{2{\mu }_{0}}$

where is the magnetic field amplitude, which is the same as the maximum magnetic field strength. One more expression for ${I}_{\text{avg}}$ in terms of both electric and magnetic field strengths is useful. Substituting the fact that $c{B}_{0}={E}_{0},$ the previous expression becomes

$I=\frac{{E}_{0}{B}_{0}}{2{\mu }_{0}}.$

We tin can use whichever of the three preceding equations is most user-friendly, considering the three equations are actually just different versions of the same result: The energy in a wave is related to aamplitude squared. Furthermore, because these equations are based on the assumption that the electromagnetic waves are sinusoidal, the top intensity is twice the average intensity; that is, ${I}_{0}=2I.$

A Laser Beam The beam from a pocket-size laboratory light amplification by stimulated emission of radiation typically has an intensity of about $1.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}{\phantom{\rule{0.2em}{0ex}}\text{W/m}}^{2}$ . Assuming that the beam is composed of plane waves, calculate the amplitudes of the electrical and magnetic fields in the beam.

Strategy Utilise the equation expressing intensity in terms of electric field to calculate the electric field from the intensity.

Solution From (Figure), the intensity of the laser beam is

$I=\frac{1}{2}c{\epsilon }_{0}{E}_{0}^{2}.$

The amplitude of the electric field is therefore

${E}_{0}=\sqrt{\frac{2}{c{\epsilon }_{0}}I}=\sqrt{\frac{2}{\left(3.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{8}\phantom{\rule{0.2em}{0ex}}\text{m/s}\right)\left(8.85\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-12}\phantom{\rule{0.2em}{0ex}}\text{F/m}\right)}\left(1.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}{\phantom{\rule{0.2em}{0ex}}\text{W/m}}^{2}\right)}=0.87\phantom{\rule{0.2em}{0ex}}\text{V/m}.$

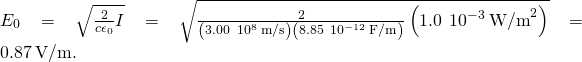
The amplitude of the magnetic field can exist obtained from (Figure):

${B}_{0}=\frac{{E}_{0}}{c}=2.9\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-9}\phantom{\rule{0.2em}{0ex}}\text{T}.$

Calorie-free Bulb Fields A light bulb emits 5.00 West of power as visible calorie-free. What are the average electric and magnetic fields from the low-cal at a altitude of 3.0 g?

Strategy Assume the bulb'due south power output P is distributed uniformly over a sphere of radius 3.0 m to summate the intensity, and from it, the electric field.

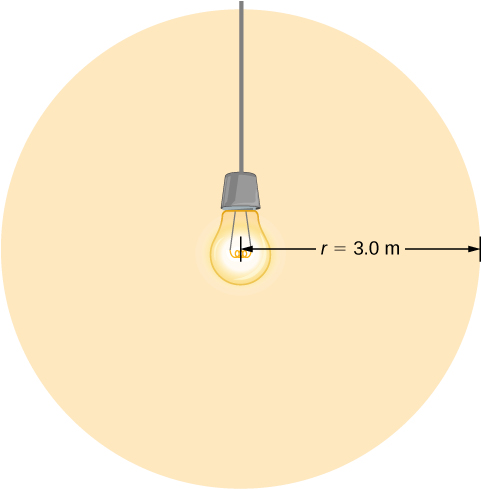
Figure shows a light bulb in the centre illuminating a circular area around it. This area has a radius of 3 m.

Solution The power radiated as visible light is then

$\begin{array}{ccc}\hfill I& =\hfill & \frac{P}{4\pi {r}^{2}}=\frac{c{\epsilon }_{0}{E}_{0}^{2}}{2},\hfill \\ \hfill {E}_{0}& =\hfill & \sqrt{2\frac{P}{4\pi {r}^{2}c{\epsilon }_{0}}}=\sqrt{2\frac{5.00\phantom{\rule{0.2em}{0ex}}\text{W}}{4\pi {\left(3.0\phantom{\rule{0.2em}{0ex}}\text{m}\right)}^{2}\left(3.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{8}\phantom{\rule{0.2em}{0ex}}\text{m/s}\right)\left(8.85\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-12}{\phantom{\rule{0.2em}{0ex}}\text{C}}^{2}\text{/N}·{\text{m}}^{2}\right)}}=5.77\phantom{\rule{0.2em}{0ex}}\text{N/C,}\hfill \\ \hfill {B}_{0}& =\hfill & {E}_{0}\text{/}c=1.92\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-8}\phantom{\rule{0.2em}{0ex}}\text{T}.\hfill \end{array}$

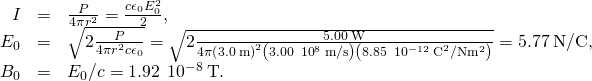
Significance The intensity I falls off as the altitude squared if the radiations is dispersed uniformly in all directions.

Radio Range A 60-kW radio transmitter on Earth sends its bespeak to a satellite 100 km away ((Figure)). At what distance in the same direction would the bespeak have the same maximum field force if the transmitter'south output ability were increased to xc kW?

In three dimensions, a signal spreads over a solid angle as information technology travels outward from its source.

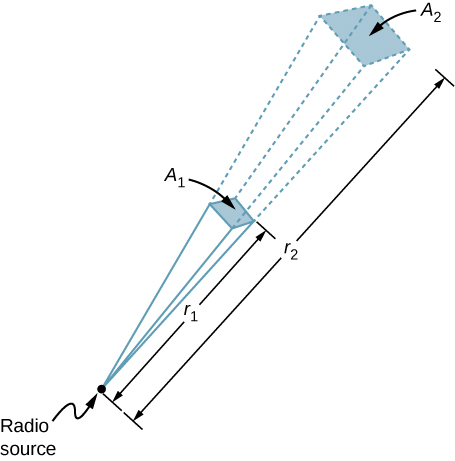
A point is labeled radio source. A small square labeled A1 is in the path of the lines radiating from the radio source. The lines continue from the corners of A1 and reach A2, a slightly bigger square. A1 is at a distance r1 from the source and A2 is at a distance R2.

Strategy The area over which the power in a particular management is dispersed increases as altitude squared, as illustrated in the effigy. Alter the power output P by a factor of (ninety kW/lx kW) and alter the surface area by the same cistron to keep $I=\frac{P}{A}=\frac{c{\epsilon }_{0}{E}_{0}^{2}}{2}$ the same. Then use the proportion of area A in the diagram to altitude squared to observe the distance that produces the calculated change in area.

Solution Using the proportionality of the areas to the squares of the distances, and solving, we obtain from the diagram

$\begin{array}{ccc}\hfill \frac{{r}_{2}^{2}}{{r}_{1}^{2}}& =\hfill & \frac{{A}_{2}}{{A}_{1}}=\frac{90\phantom{\rule{0.2em}{0ex}}\text{W}}{60\phantom{\rule{0.2em}{0ex}}\text{W}},\hfill \\ \hfill {r}_{2}& =\hfill & \sqrt{\frac{90}{60}}\left(100\phantom{\rule{0.2em}{0ex}}\text{km}\right)=122\phantom{\rule{0.2em}{0ex}}\text{km}.\hfill \end{array}$

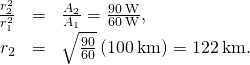
Significance The range of a radio signal is the maximum distance between the transmitter and receiver that allows for normal operation. In the absenteeism of complications such as reflections from obstacles, the intensity follows an inverse square law, and doubling the range would require multiplying the ability past four.

Summary

The energy carried by whatsoever wave is proportional to its amplitude squared. For electromagnetic waves, this ways intensity can be expressed as

$I=\frac{c{\epsilon }_{0}{E}_{0}^{2}}{2}$

where I is the average intensity in ${\text{W/m}}^{2}$ and ${E}_{0}$ is the maximum electric field forcefulness of a continuous sinusoidal moving ridge. This tin can also exist expressed in terms of the maximum magnetic field strength ${B}_{0}$ equally

$I=\frac{c{B}_{0}^{2}}{2{\mu }_{0}}$

and in terms of both electric and magnetic fields every bit

$I=\frac{{E}_{0}{B}_{0}}{2{\mu }_{0}}.$

The three expressions for ${I}_{\text{avg}}$ are all equivalent.

Conceptual Questions

When you stand outdoors in the sunlight, why tin you feel the free energy that the sunlight carries, but not the momentum it carries?

The corporeality of free energy (about ${100\phantom{\rule{0.2em}{0ex}}\text{W/m}}^{2}$ ) is tin can speedily produce a considerable change in temperature, just the light pressure (about $3.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-7}{\text{N/m}}^{2}$ ) is much too small to detect.

How does the intensity of an electromagnetic wave depend on its electric field? How does it depend on its magnetic field?

What is the physical significance of the Poynting vector?

Information technology has the magnitude of the energy flux and points in the direction of wave propagation. It gives the management of energy menstruum and the amount of energy per area transported per second.

A 2.0-mW helium-neon laser transmits a continuous beam of red lite of cantankerous-sectional expanse $0.25\phantom{\rule{0.2em}{0ex}}{\text{cm}}^{2}$ . If the beam does not diverge appreciably, how would its rms electric field vary with altitude from the laser? Explain.

Problems

While outdoors on a sunny solar day, a educatee holds a large convex lens of radius 4.0 cm to a higher place a canvass of paper to produce a vivid spot on the newspaper that is 1.0 cm in radius, rather than a sharp focus. By what factor is the electric field in the bright spot of lite related to the electric field of sunlight leaving the side of the lens facing the newspaper?

A aeroplane electromagnetic wave travels northward. At 1 instant, its electric field has a magnitude of 6.0 V/thousand and points eastward. What are the magnitude and direction of the magnetic field at this instant?

The magnetic field is downward, and it has magnitude $2.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-8}\text{T}$ .

The electric field of an electromagnetic wave is given by
$E=\left(6.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\phantom{\rule{0.2em}{0ex}}\text{V/m}\right)\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}\left[2\pi \left(\frac{x}{18\phantom{\rule{0.2em}{0ex}}\text{m}}-\frac{t}{6.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-8}\phantom{\rule{0.2em}{0ex}}\text{s}}\right)\right]\stackrel{^}{j}.$
Write the equations for the associated magnetic field and Poynting vector.

A radio station broadcasts at a frequency of 760 kHz. At a receiver some distance from the antenna, the maximum magnetic field of the electromagnetic moving ridge detected is $2.15\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-11}\text{T}$ .
(a) What is the maximum electrical field? (b) What is the wavelength of the electromagnetic moving ridge?

a. $6.45\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}\phantom{\rule{0.2em}{0ex}}\text{V/m;}$ b. 394 m

The filament in a articulate incandescent light seedling radiates visible low-cal at a power of 5.00 West. Model the glass part of the bulb as a sphere of radius ${r}_{0}=3.00\phantom{\rule{0.2em}{0ex}}\text{cm}$ and calculate the amount of electromagnetic energy from visible lite inside the bulb.

At what distance does a 100-W lightbulb produce the same intensity of light as a 75-W lightbulb produces 10 chiliad away? (Assume both have the same efficiency for converting electrical energy in the circuit into emitted electromagnetic energy.)

11.v m

An incandescent light bulb emits only 2.6 W of its ability as visible lite. What is the rms electric field of the emitted calorie-free at a altitude of 3.0 m from the seedling?

A 150-W lightbulb emits 5% of its energy as electromagnetic radiation. What is the magnitude of the average Poynting vector 10 chiliad from the bulb?

$5.97\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}{\phantom{\rule{0.2em}{0ex}}\text{W/m}}^{2}$

A minor helium-neon light amplification by stimulated emission of radiation has a power output of 2.five mW. What is the electromagnetic energy in a 1.0-thou length of the axle?

At the height of Earth'southward atmosphere, the fourth dimension-averaged Poynting vector associated with sunlight has a magnitude of most $1.4\phantom{\rule{0.2em}{0ex}}{\text{kW/m}}^{2}.$
(a) What are the maximum values of the electrical and magnetic fields for a moving ridge of this intensity? (b) What is the total power radiated by the lord's day? Assume that the Earth is $1.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{11}\text{m}$ from the Sunday and that sunlight is composed of electromagnetic plane waves.

$\text{a.}\phantom{\rule{0.2em}{0ex}}{E}_{0}=1027\phantom{\rule{0.2em}{0ex}}\text{V/m},{B}_{0}=3.42\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-6}\text{T};\phantom{\rule{0.2em}{0ex}}\text{b.}\phantom{\rule{0.2em}{0ex}}3.96\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{26}\phantom{\rule{0.2em}{0ex}}\text{W}$

What is the intensity of an electromagnetic wave with a peak electrical field forcefulness of 125 V/m?

$20.8\phantom{\rule{0.2em}{0ex}}{\text{W/m}}^{2}$

Assume the helium-neon lasers ordinarily used in student physics laboratories have power outputs of 0.500 mW. (a) If such a laser beam is projected onto a circular spot i.00 mm in diameter, what is its intensity? (b) Find the pinnacle magnetic field strength. (c) Notice the peak electric field strength.

An AM radio transmitter broadcasts 50.0 kW of power uniformly in all directions. (a) Bold all of the radio waves that strike the ground are completely absorbed, and that there is no absorption by the atmosphere or other objects, what is the intensity 30.0 km away? (Hint: One-half the power volition exist spread over the area of a hemisphere.) (b) What is the maximum electric field strength at this distance?

a. $4.42\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{‒6}{\phantom{\rule{0.2em}{0ex}}\text{W/m}}^{2}$ ; b. $5.77\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{‒2}\phantom{\rule{0.2em}{0ex}}\text{V/m}$

Suppose the maximum prophylactic intensity of microwaves for human being exposure is taken to be $1.00{\phantom{\rule{0.2em}{0ex}}\text{W/m}}^{2}$ . (a) If a radar unit leaks ten.0 W of microwaves (other than those sent by its antenna) uniformly in all directions, how far away must you be to be exposed to an intensity considered to be rubber? Assume that the power spreads uniformly over the surface area of a sphere with no complications from absorption or reflection. (b) What is the maximum electrical field forcefulness at the safe intensity? (Note that early radar units leaked more than modern ones do. This caused identifiable health problems, such as cataracts, for people who worked well-nigh them.)

A 2.50-k-bore university communications satellite dish receives Goggle box signals that have a maximum electric field strength (for one channel) of $7.50\phantom{\rule{0.2em}{0ex}}\text{μV/m}$ (see below). (a) What is the intensity of this wave? (b) What is the ability received past the antenna? (c) If the orbiting satellite broadcasts uniformly over an area of $1.50\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{13}{\phantom{\rule{0.2em}{0ex}}\text{m}}^{2}$ (a large fraction of North America), how much power does information technology radiate?

Figure shows waves incident on a dish antenna.

a. $7.47\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-14}{\phantom{\rule{0.2em}{0ex}}\text{W/m}}^{2}$ ; b. $3.66\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{\text{−}13}\phantom{\rule{0.2em}{0ex}}\text{W}$ ; c. one.12 W

Lasers can exist synthetic that produce an extremely loftier intensity electromagnetic moving ridge for a brief time—called pulsed lasers. They are used to initiate nuclear fusion, for example. Such a laser may produce an electromagnetic wave with a maximum electric field strength of $1.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{11}\phantom{\rule{0.2em}{0ex}}\text{V}\text{/}\text{m}$ for a time of 1.00 ns. (a) What is the maximum magnetic field forcefulness in the wave? (b) What is the intensity of the beam? (c) What energy does information technology evangelize on an $1.00{\text{-mm}}^{2}$ area?

Glossary

Poynting vector: vector equal to the cross product of the electric-and magnetic fields, that describes the catamenia of electromagnetic free energy through a surface

mcgheeexpont.blogspot.com

Source: https://opentextbc.ca/universityphysicsv2openstax/chapter/energy-carried-by-electromagnetic-waves/

McGhee Expont